В геометрії після точки пряма лінія, мабуть, є самим простим елементом. Його використовують при побудові будь-яких складних фігур на площині та у тривимірному просторі. У цій статті розглянемо загальне рівняння прямої і розв’яжемо декілька задач з його використанням. Приступимо!
Пряма лінія в геометрії
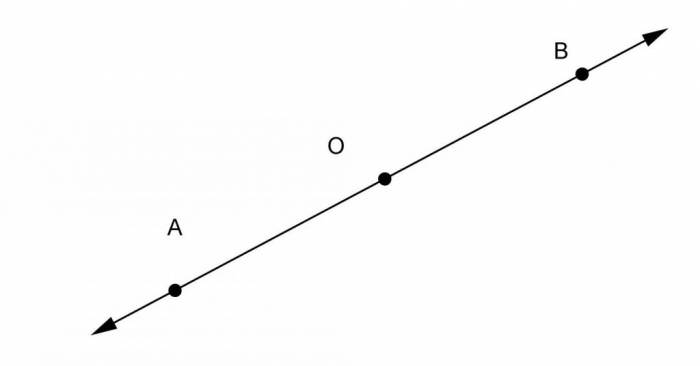
Кожен знає, що такі фігури, як прямокутник, трикутник, призма, куб і так далі утворені пересічними прямими лініями. Під пряма в геометрії вважається одновимірний об’єкт, який може бути отриманий шляхом перенесення певної точки на має одне і те ж або протилежний напрямок вектор. Щоб краще зрозуміти це визначення, уявімо, що є деяка точка P в просторі. Візьмемо довільний вектор u в цьому просторі. Тоді будь-яка точка Q прямий може бути отримана в результаті таких математичних операцій:
Q = P + λ*u.
Тут λ – це довільне число, яке може бути позитивним і негативним. Якщо рівність вище записати через координати, то ми отримаємо наступне рівняння прямої:
(x, y, z) = (x0, y0, z0) + λ*(a, b, c).
Це рівняння називається рівнянням прямої у векторній формі. А вектор u називається направляючим.