Кожен школяр старших класів знає про таких просторових фігурах, як куля, циліндр, конус, піраміда і призма. З цієї статті ви дізнаєтеся про те, що собою являє трикутна призма, і якими властивостями вона характеризується.
Яку фігуру розглянемо в статті?
Трикутна призма є найпростішим представником класу призм, який має меншу кількість сторін, вершин і ребер, ніж яка-небудь інша подібна просторова фігура. Ця призма утворена двома трикутниками, які можуть мати довільну форму, але які обов’язково повинні бути рівні один одному і перебувати в рівнобіжних площинах в просторі, і трьома параллелограммами, не рівними між собою в загальному випадку. Для наочності нижче наведена описана фігура.
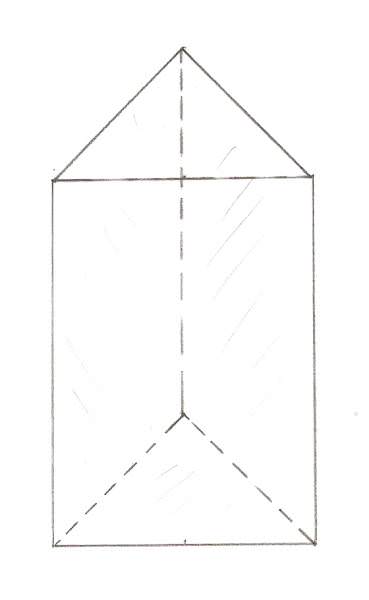
Як можна отримати трикутну призму? Дуже просто: слід взяти трикутник і перенести його на деякий вектор в просторі. Потім однакові вершини двох трикутників з’єднати відрізками. Так ми отримаємо каркас фігури. Якщо тепер уявити, що цей каркас обмежує суцільні боку, то ми отримаємо зображену об’ємну фігуру.












