Фігур обертання в геометрії приділяється особлива увага при вивченні їх характеристик і властивостей. Однією з них є усічений конус. Дана стаття має на меті відповісти на питання, за якою формулою можна обчислити площу усіченого конуса.
Про який фігурі піде мова?
Перш ніж описувати площа усіченого конуса, необхідно дати точне геометричне визначення даної фігури. Усіченим називається такий конус, який виходить в результаті відсікання площиною вершини звичайного конуса. В цьому визначенні слід підкреслити ряд нюансів. По-перше, площина перерізу повинна бути паралельною площині основи конуса. По-друге, вихідна фігура повинна являти собою круговий конус. Звичайно, це може бути еліптичний, гіперболічний і інший вид фігури, але в даній статті обмежимося розглядом тільки кругового конуса. Останній наведено нижче на малюнку.
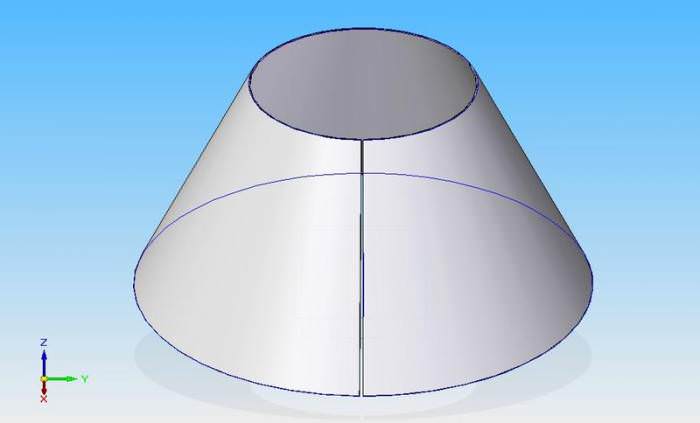
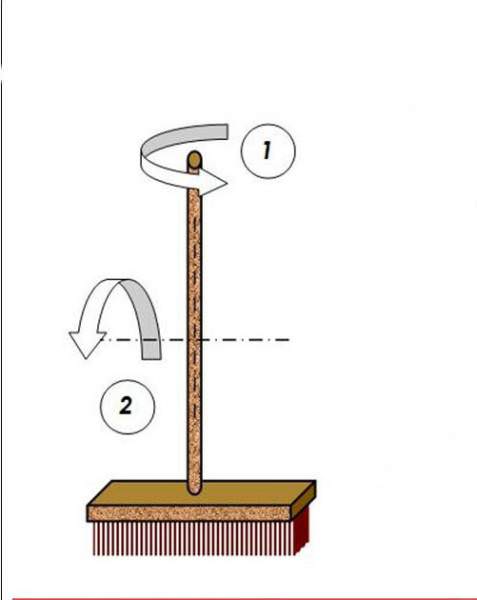
Нескладно здогадатися, що його можна отримати не тільки за допомогою перерізу площиною, але і за допомогою операції обертання. Для цього необхідно взяти трапецію, має два прямих кута, і обертати її навколо боку, що прилягає до цих прямим кутам. В результаті підстави трапеції стануть радіусами основ зрізаного конуса, а похила-бічна сторона трапеції описує конічну поверхню.
Розгортка фігури
Розглядаючи площа поверхні зрізаного конуса, корисно привести його розгортку, тобто зображення поверхні об’ємної фігури на площині. Нижче зображена розгортка досліджуваної фігури з довільними параметрами.
Видно, що площа фігури утворена трьома складовими: два кола і один усічений круговий сегмент. Очевидно, що для визначення шуканої площі, необхідно скласти площі всіх названих фігур. Займемося вирішенням цієї задачі в наступному пункті.
Площа усіченого конуса
Щоб легше було зрозуміти подальші міркування, введемо наступні позначення:
- r1, r2 – радіуси великого і малого підстав відповідно;
- h – висота фігури;
- g – твірна конуса (довжина похилої сторони трапеції).
Площа підстав усіченого конуса розрахувати нескладно. Запишемо відповідні вирази:
So1 = pi*r12;
So2 = pi*r22.
Площа частини кругового сегмента визначити дещо складніше. Якщо уявити, що центр цього кругового сектора не вирізано, тоді його радіус дорівнює величині G. Обчислити її нескладно, якщо розглянути відповідні подібні прямокутні трикутники конуса. Вона дорівнює:
G = r1*g/(r1-r2).
Тоді площа цілого кругового сектора, який побудований на радіусі G і який спирається на дугу довжиною 2*pi*r1, буде дорівнює:
S1 = pi*r1*G = pi*r12*g/(r1-r2).
Тепер визначимо площу малого кругового сектора S2, яку потрібно буде відняти з S1. Вона дорівнює:
S2 = pi*r2*(G – g) = pi*r2*(r1*g/(r1-r2) – g) = pi*r22*g/(r1-r2).
Площа конічної усіченої поверхні Sb дорівнює різниці S1 і S2. Отримуємо:
Sb = S1 – S2 = pi*r12*g/(r1-r2) – pi*r22*g/(r1-r2) = pi*g*(r1+r2).
Незважаючи на дещо громіздкі обчислення, ми отримали досить простий вираз для площі бічної поверхні фігури.
Склавши площі підстав і Sb, приходимо до формули площі усіченого конуса:
S = So1 + So2 + Sb = pi*r12 + pi*r22 + pi*g*(r1+r2).
Таким чином, для розрахунку величини S досліджуваної фігури необхідно знати три її лінійних параметра.
Приклад завдання
Прямий круговий конус радіусом 10 см і заввишки 15 см був обрізаний площиною так, що вийшов правильний усічений конус. Знаючи, що відстань між підставами усіченої фігури дорівнює 10 см, необхідно знайти площу її поверхні.
Щоб скористатися формулою площі усіченого конуса, необхідно знайти три його параметра. Один ми знаємо:
r1 = 10 див.
Два інших нескладно розрахувати, якщо розглянути подібні прямокутні трикутники, які отримуються в результаті осьового перерізу конуса. З урахуванням умови задачі одержуємо:
r2 = 10*5/15 = 3,33 див.
Нарешті, напрямна усіченого конуса g буде дорівнює:
g = √(102 + (r1-r2)2) = 12,02 див.
Тепер можна підставити величини r1, r2 і g у формулу для S:
S = pi*r12 + pi*r22 + pi*g*(r1+r2) = 851,93 см2.
Шукана площа поверхні фігури приблизно дорівнює 852 см2.
