Важливим розділом геометрії, який вивчають у старших класах шкіл, є стереометрія. Об’єкти її дослідження – це характеристики і властивості фігур у тривимірному просторі. Дана стаття присвячена питанню площі повної поверхні призми.
Про якому геометричному об’єкті піде мова?
Перш ніж розглядати у призми площа повної поверхні, необхідно пояснити, що вона собою являє. Під нею в стереометрії розуміють об’ємне тіло, яке обмежене кількома гранями. Дві з них лежать у паралельних площинах і є абсолютно однаковими, вони називаються підставами фігури. Інші грані пов’язують відповідні сторони підстав між собою і називаються бічними. Щоб зрозуміти, яка фігура описана вище, наведемо приклад першого періоду призми.
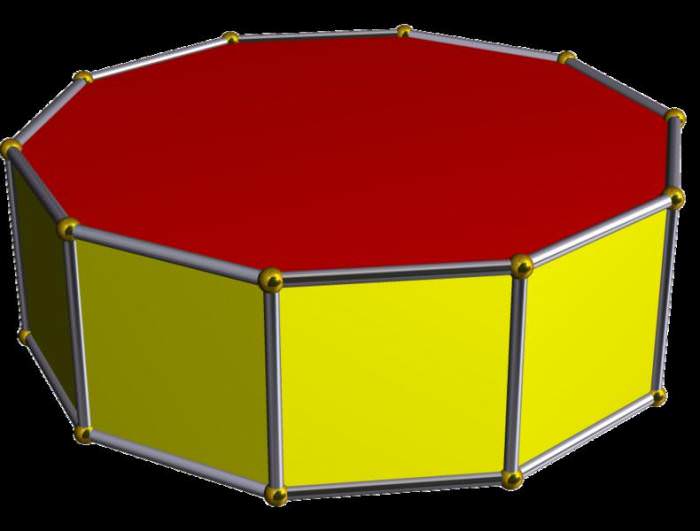
Так вона називається через числа кутів в підставі. З малюнка видно, якщо 10 – це число кутів багатокутного підстави, то кількість сторін фігури дорівнює 10+2 = 12, число її вершин становить 2*10 = 20, а кількість ребер дорівнює 3*10 = 30. На малюнку бічні грані являють собою квадрати. В загальному випадку ці межі є параллелограммами.
Всі представники класу призм класифікуються за кількома ознаками. Головним чином, ці ознаки визначаються типом багатокутного підстави. Так, воно може бути увігнутих і опуклих, правильним і довільної форми. Якщо всі сторони бічні є прямокутниками або квадратами, то говорять про прямі фігурах. Якщо ж деякі з цих сторін будуть параллелограммами довільного типу, то призма називається похилою. Особливий клас – це правильні геометричні об’єкти. Крім того, що вони є прямими, їх підстави являють собою рівносторонні і рівнокутні плоскі многокутники. На малюнку нижче наведений широкий набір правильних призм.