Циліндр є однією з поширених форм просторових тіл, з якими ми стикаємося щодня. Дійсно, гуртка, таблетка, димар, труба та інші предмети мають циліндричну форму. У цій статті розглянемо питання, як розрахувати обсяг циліндра, використовуючи різні відомі параметри цієї фігури.
Визначення циліндра в геометрії

Перш ніж переходити до відповіді на питання, як розрахувати обсяг циліндра, розберемося, з якою фігурою ми маємо справу.
З геометричної точки зору циліндр утворений двома одновимірними елементами. Перший – це крива, яка є направляючою. Другий – це прямий відрізок, який називається твірною. Коли відрізок не знаходиться в площині кривої, якщо його один кінець з’єднати з кривою і переміщати паралельно самій собі вздовж неї, то ми отримаємо циліндричну поверхню.
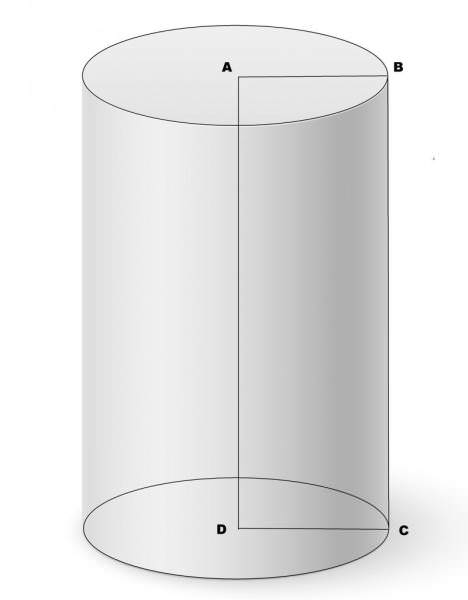
Під надане визначення підходить безліч просторових фігур, включаючи гіперболічні, параболічні та еліптичні циліндри. Тим не менш в даній статті будемо розглядати тільки круглий прямий циліндр. Круглим він називається по причині того, що його заснування є колами (напрямна – окружність), а прямий він тому, що відрізок утворює перпендикулярний підстав. Для наочності описаний циліндр показаний на малюнку.