Призма є однією з найвідоміших постатей, які вивчаються у курсі стереометрії в загальноосвітніх школах. Щоб вміти розраховувати різні характеристики фігур цього класу, необхідно знати, які види призм існують. Розглянемо це питання докладніше.
Призма в стереометрії
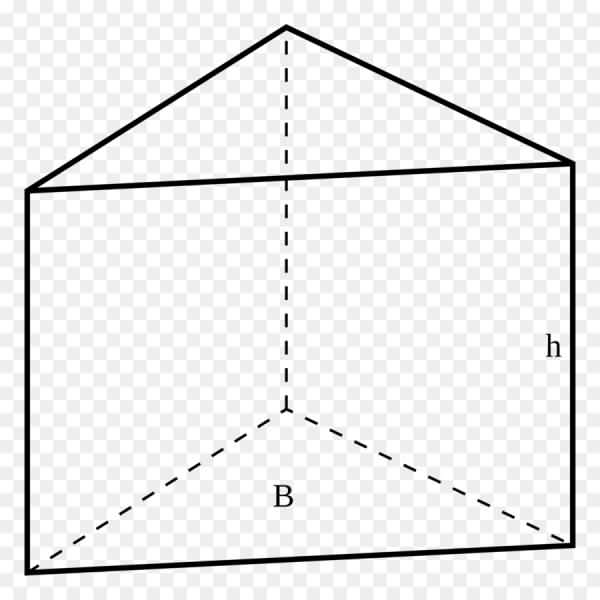
Насамперед дамо визначення згаданого класу фігур. Призмою є будь-многогранник, який складається з двох паралельних багатокутних підстав, які між собою з’єднані параллелограммами.
Отримати цю фігуру можна так: слід вибрати довільний багатокутник на площині, а потім переміщати його на довжину будь-якого вектора, який не належить вихідної площини многокутника. В ході такого паралельного переміщення сторони багатокутника опишуть бічні грані майбутньої призми, а кінцеве положення багатокутника стане другою підставою фігури. Описаним способом може бути отримана довільного виду призма. Малюнок нижче демонструє трикутну призму.