Стереометрія-це розділ геометрії, який вивчає різні властивості фігур у просторі тривимірної системи координат. Однією з таких постатей є прямокутна призма. Що вона собою являє, і які властивості для неї характерні, розглянемо в цій статті.
Прямокутна Призма в стереометрії
Кожна людина знайомий з цієї досконалої геометричною фігурою. Під нею розуміють об’ємний об’єкт, який складається з шести прямокутників у загальному випадку, причому всі вони попарно рівні. Отримати в просторі цю призму нескладно. Необхідно взяти довільний прямокутник і перенести його паралельно самій собі вздовж відрізка, перпендикулярного вихідного прямокутника. В результаті вийде фігура, зображена нижче на малюнку.
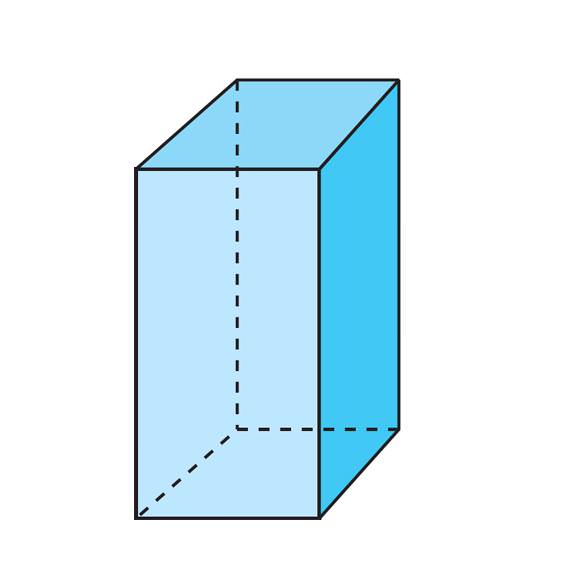
Прямокутна призма називається параллелепипедом. Якщо її основу буде квадратом, то вона стане правильною призмою, у якої бічні прямокутники будуть рівні між собою. Якщо у правильної призми сторона підстави співпаде з висотою (довжиною бічного ребра), тоді ми отримаємо фігуру куб.












