Кожна людина чув про великих єгипетських кам’яних спорудах, головним з яких є піраміда Хеопса. У курсі стереометрії розглядають характеристики різних пірамід. Одним з важливих параметрів фігури є площа бічної поверхні. За якою формулою площа бічної поверхні піраміди слід розраховувати, розповість ця стаття.
Що собою являє піраміда в геометрії?
Перш ніж говорити про піраміду і формули площі бічної поверхні, дамо визначення самої фігури. Під нею вважають об’ємний многогранник, який складається з одного n-вугільного підстави та n трикутників. Всі трикутники мають одну спільну з підставою сторону, а також перетинаються в точці, яка називається вершиною. Нижче показана довільна чотирикутна піраміда:
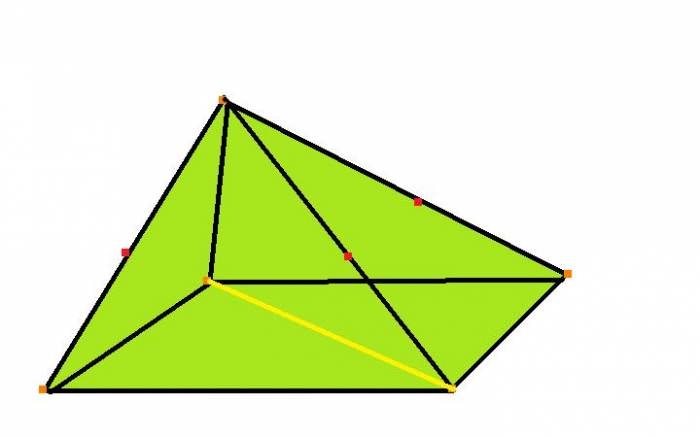
Отримати піраміду досить просто. Для цього необхідно вибрати плоский багатокутник і з’єднати всі його вершини з єдиною точкою простору. Обов’язкова умова – ця точка не повинна лежати на площині.
Будь-яка піраміда складається з:
- граней, яких у неї n+1 штука;
- вершин (n+1 штука);
- ребер (2*n штук).
Причому всі названі елементи бувають двох типів: ті, які відносяться до основи, і ті, які належать бічній поверхні.